[Algorithm] Bubble Sort (거품정렬) by Swift
안녕하세요! Joy 입니다. 오늘부터 알고리즘을 하나씩 정리해두려고 해요!
참고 자료는 하단에도 기재하겠지만, gyoogle님의 블로그를 참조했고, 예시 코드는 Swift로 제가 직접 작성했어요!
(gyoogle님 글을 통해 다시 한번 알고리즘을 공부하고 정리하게 되었어요 감사합니다 : ))
알고리즘들을 하나씩 정리하고, 이후에는 백준과 프로그래머스 문제를 다시 한번 차근차근 복습하려고 합니다.
알고리즘은 정말 기본이잖아요!
저도 다시 기본으로 돌아가서 공부하는 마음으로 시작해보겠습니다!
오류와 오타는 댓글로 지적해주세요!
개념
- Bubble Sort는 Selection Sort와 유사한 알고리즘으로 서로 인접한 두 원소의 대소를 비교하고, 조건에 맞지 않다면 자리를 교환하며 정리하는 알고리즘이다.
여기까지만 봐도 왜 이름이 "버블" 정렬인지 알 수 있죠?
계속해서 교환.. 교환.. 뭔가 버블버블 하지 않나요? (아님)
Process (Ascending)
- 1회전에 첫번째 원소와 두번째 원소를, 두번째 원소와 세번째 원소를, 네번째 원소와 다섯번째 원소를.. 이런식으로 마지막 - 1번째 원소와 마지막 원소를 비교하여 조건에 맞지 않는다면 서로 교환한다.
- 1회전을 수행하고 나면 가장 큰 원소가 맨 뒤로 이동하므로 2회전에서는 맨 끝에 있는 원소는 정렬에서 제외되고, 2회전을 수행하고 나면 끝에서 두번째 원소까지는 정렬에서 제외한다. 이렇게 정렬을 1회전 수행할 때마다 정렬에서 제외되는 원소가 하나씩 늘어난다.
그럼 이 프로세스를 보고 직접 한번 버블정렬을 하는 메소드를 한번 작성해보세요!
제가 작성한 메소드는 이렇습니다!
func bubbleSort(arrOriginal: [Int]) {
var tmp = 0
var arr = arrOriginal
// 1. 제외될 원소의 갯수 의미
for i in 0..<arr.count {
// 2. 원소를 비교할 index 뽑을 반복문
for j in 1..<arr.count - i {
//3. 두 원소 비교해서 바꾸기..
if arr[j-1] > arr[j] {
tmp = arr[j-1]
arr[j-1] = arr[j]
arr[j] = tmp
}
}
}
print(arr)
}
bubbleSort(arrOriginal: [5,2,1,30,4])Swift는 매개변수로 주어지는 값은 let 이기 때문에 arr이라는 변수에 재할당 해주었어요.
아무 생각 없이 arrOriginal 의 인덱스에 접근해서 값을 swap 해주면

이런 에러를 만날 수 있어요. 당연함.
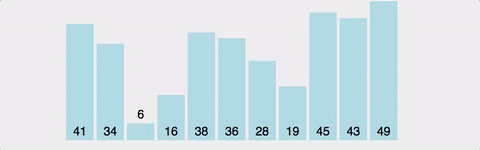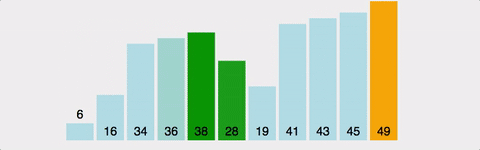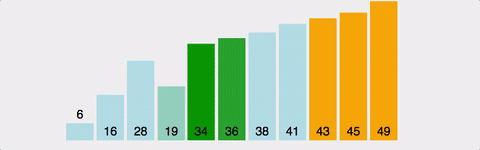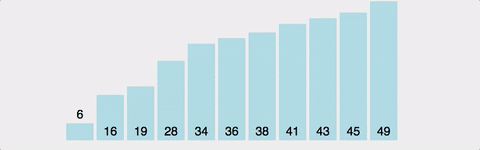
Bubble Sort 시각적으로 확인하기
제가 gyoogle님 블로그에서 정말 좋았던 항목입니다. 다시 한번 감사합니다 !!!!!
이 gif 를 보면 뭔가 시각적으로 확 보이니까 내가 어떤 알고리즘을 공부하고 있는지 알 수 있겠더라구요!
시간복잡도
(n-1) + (n-2) + (n-3) + ... + 2 + 1 => n(n-1)/2 => O(n^2)
버블정렬은 정렬이 되어있던 안되어있던 2개의 원소를 비교하기 때문에 최선, 평균, 최악의 경우 모든 시간복잡도가 O(n^2)으로 동일하다.
시간복잡도란?
알고리즘의 수행 시간을 평가하는 것.
최선 / 최악 / 평균 세가지로 나타내며, 알고리즘의 성능은 최악의 경우로 판단한다.
공간복잡도
주어진 배열 안에서 교환을 통해 정렬이 수행되므로 O(n) 이다.
공간복잡도란?
알고리즘에서 사용하는 메모리의 양을 나타내는 것
장점
- 구현이 매우 간단하고 소스코드가 직관적이다.
- 정렬하고자 하는 배열 안에서 교환하는 방식이므로 다른 메모리 공간을 필요로 하지 않음 -> 제자리 정렬
- 안정 정렬이다.
단점
- 시간복잡도 최악! 비효율적
- 정렬되어있지 않은 원소가 정렬됐을 때의 자리로 가기 위해서 교환 연산이 많이 일어남.
간단한 알고리즘인 버블 정렬을 정리해보았습니다!
첫 글인 만큼 시간복잡도와 공간복잡도에 대해 간단한 설명도 추가해 보았는데요, 다음에 기회가 된다면 시간복잡도/공간복잡도 관련 포스팅도 한번 해볼게요!!!!
오늘도 읽어주셔서 감사합니다!
참고 출처 : https://gyoogle.dev/blog/algorithm/Selection%20Sort.html