안녕하세요! Joy 입니다.
저는 어저께 3차 백신 (부스터샷) 을 맞아서 회사도 연차내고 아주 푹 쉬느라고 포스팅을 못했어요
저와의 약속을 지키려고 매일 1일 1포스팅을 하려고 했는데.. 흐흑
그래도 생각보다 많이 아프진 않더라고요!
하루 푹 자고 나니까 말끔히 나아버렸습니다 히히
그럼 오늘은 세번째 알고리즘인 삽입 정렬을 공부해보려고 해요!
시~~작~~합니다~~~~
개념
- 손 안의 카드를 정렬하는 방법과 유사하다.
- Insertion Sort는 Selection Sort와 유사하지만 조금 더 효율적인 정렬 알고리즘이다.
- 두번재 원소부터 시작하여 그 앞 (왼쪽)의 원소들과 비교하여 삽입할 위치를 지정한 후, 원소를 뒤로 옮기고 지정된 자리에 자료를 삽입하여 정렬하는 알고리즘이다.
- 최선의 경우 O(N)이라는 빠른 효율성을 가지고 있어 다른 정렬 알고리즘의 일부로 사용될 만큼 좋은 정렬 알고리즘이다.
Process
- 정렬은 2번째 위치(index)의 값을 temp에 저장한다.
- temp와 이전에 있는 원소들과 비교하며 삽입해나간다.
- '1'번으로 돌아가 다음 위치(index)의 값을 temp에 저장하고, 반복한다.
Example Code
func insertionSort(originalArr: [Int]) {
var arr = originalArr
// 1. 처음에는 두번째 위치의 인덱스 값을 tmp에 저장
for i in 1..<arr.count {
// tmp에는 임시로 인덱스 값의 원소를 저장하고, prev 에는 이전 위치를 저장
let tmp = arr[i]
var prev = i - 1;
// 이전 위치를 가리키는 prev가 음수가 되지 않고, 이전 위치의 값이 1번에서 선택한 값보다 크다면 서로 값을 교환해주고 prev를 더 이전 위치를 가리키도록 함
// 2. tmp와 이전에 있는 원소들과 비교하며 삽입
while prev >= 0 && arr[prev] > tmp {
arr[prev + 1] = arr[prev]
prev -= 1
}
// 반복문이 끝나고 난 뒤 prev는 현재 tmp 값보다 작은 값들 중 가장 큰 값의 위치를 가리키게 된다. 따라서 prev+1에 tmp 값을 삽입
// 3. 1번으로 돌아가 다음 위치의 인덱스 값을 tmp에 저장하고 반복한다.
arr[prev + 1] = tmp
}
print(arr)
}
insertionSort(originalArr: [5,2,1,30,10,7])
Insertion Sort 시각적으로 확인하기
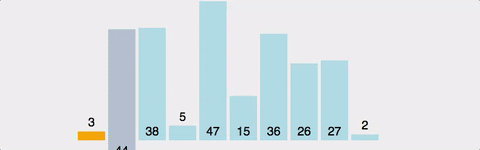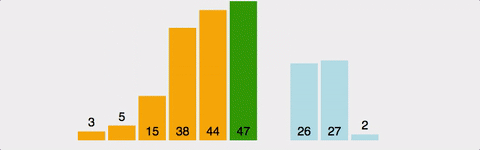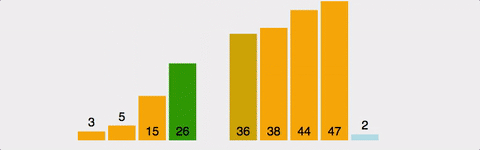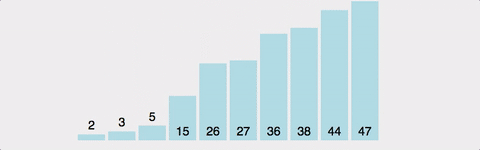
시간복잡도
- 최악의 경우 (역으로 정렬되어 있을 경우)
- (n-1) + (n-2) + ... + 2 + 1 => n(n-1)/2 => O(n^2)
- 하지만 모두 정렬이 되어있는 경우 한번씩 밖에 비교를 안하므로 O(n)의 시간복잡도를 가지게 된다.
- 또한 이미 정렬되어있는 배열에 자료를 하나씩 삽입/제거 하는 경우에는 현실적으로 최고의 정렬 알고리즘이 되는데 탐색을 제외한 오버헤드가 매우 적기 때문이다.
- 최선의 경우는 O(n)의 시간복잡도를 가지고 평균,최악의 경우 O(n^2)의 시간복잡도를 갖게 된다.
공간복잡도
- 주어진 배열안에서 교환을 통해 정렬이 수행되므로 O(n)이다.
장점
- 알고리즘이 단순하다.
- 대부분의 원소가 이미 정렬되어 있는 경우 매우 효율적일 수 있다.
- 정렬하고자 하는 배열 안에서 교환하는 방식이므로 다른 메모리 공간을 필요로 하지 않는다.
- 안정 정렬이다.
- 선택정렬, 버블정렬과 같은 O(n^2) 알고리즘에 비하여 상대적으로 빠르다.
단점
- 평균과 최악의 시간복잡도가 비효율적이다.
- 배열의 길이가 길어질 수록 비효율적이다. (버블, 선택 정렬도 마찬가지.)
Selection Sort와 Insertion Sort 는 K번째 반복 이후 첫번째 K 요소가 정렬된 순서로 온다는 점에서 유사합니다. 하지만 Selection Sort는 K+1번째 요소를 찾기 위해 나머지 모든 요소들을 탐색하지만 Insertion Sort는 K+1번째 요소를 배치하는데 필요한 만큼의 요소만 탐색하기 때문에 훨씬 효율적으로 실행된다는 차이가 있습니다!
이걸 쓰면서도 저도 Insertion Sort와 Selection Sort가 헷갈려서 계속 다시 봤네요.. (허접)
내친김에 관련 백준 문제라도 풀어보려고요!
오늘도 읽어주셔서 감사합니다!
참고 출처 : https://gyoogle.dev/blog/algorithm/Insertion%20Sort.html
반응형
'🔡 Algorithm' 카테고리의 다른 글
| [Algorithm] 퀵정렬 (Quick Sort) by Swift (0) | 2022.01.16 |
|---|---|
| [Algorithm] Selection Sort (선택정렬) by Swift (0) | 2022.01.11 |
| [Algorithm] Bubble Sort (거품정렬) by Swift (0) | 2022.01.10 |