안녕하세요! Joy 입니다.
오늘 늦잠을 잤더니 아주 좋은데 사실 아직 잠이 덜깼어요...
오늘은 오타가 있어도... 나는 몰라요! (무책임)
아무튼 그래서 오늘 공부할 알고리즘은 퀵정렬 입니다!
퀵정렬은 사실 개념 자체는 그리 어렵지 않은데 알고리즘 구현시에 재귀를 활용하다 보니까 (저는) 많이 헷갈리더라구요..
아직 알고리즘을 통달하려면 멀었나 봅니다..
그럼 시작해볼게요!
개념
- 분할 정복 방법을 통해 주어진 배열을 정렬한다.
[분할 정복 방법]
문제를 작은 두개의 문제로 분리하고 각각 해결한 다음, 결과를 모아서 문제를 해결하는 전략- Quick Sort는 불안정 정렬에 속하며, 다른 원소와의 비교만으로 정렬을 수행하는 비교 정렬에 속한다. 또한 merge sort와 달리 quick sort는 배열을 배균등하게 분열한다.
Process
- 배열 가운데서 하나의 원소를 고른다. 이렇게 고른 원소를 피벗(pivot)이라고 한다.
- 피벗 앞에는 피벗보다 값이 작은 모든 원소들이 오고, 피벗 뒤에는 피벗보다 값이 큰 모든 원소들이 오도록 피벗을 기준으로 배열을 둘로 나눈다. 이렇게 배열을 둘로 나누는 것을 분할이라고 한다. 분할을 마친 뒤에 피벗은 더이상 움직이지 않는다.
- 분할된 두 개의 작은 배열에 대해 재귀적으로 이 과정을 반복한다.
Example Code
// 퀵정렬
func quickSort(array: [Int]) -> [Int] {
guard let first = array.first, array.count > 1 else { return array }
let pivot = first
let left = array.filter { $0 < pivot }
let right = array.filter { $0 > pivot }
return quickSort(array: left) + [pivot] + quickSort(array: right)
}
print(quickSort(array: [10,1,4,3,5]))
Quick Sort 시각적으로 확인하기
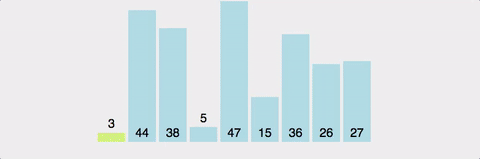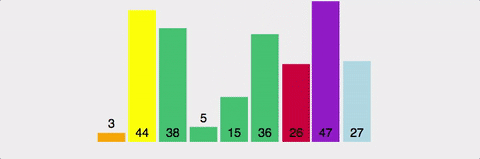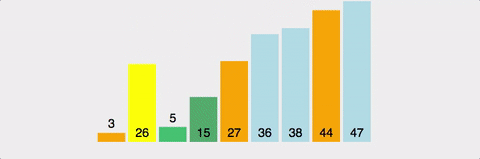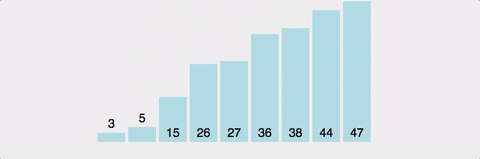
시간복잡도
- 최선의 경우 O(nlog₂n)
- 각 순환 호출 단계의 비교 연산 (n)
- 각 순환 호출에서는 전체 리스트의 대부분의 레코드를 비교해야 하므로 평균 n번 정도의 비교가 이루어짐
- 따라서 최선의 시간복잡도는 순환 호출의 깊이 * 각 순환 호출 단계의 비교 연산 = nlog₂n 가 된다.
- 이동 횟수는 비교 횟수보다 적으므로 무시할 수 있다.
- 최악의 경우 O(n^2)
- 최악의 경우는 정렬하고자 하는 배열이 오름차순 정렬되어있거나 내림차순 정렬되어있는 경우
- 비교횟수 (n) -> 순환 호출의 깊이
- 각 순환 호출 단계의 비교 연산 (n)
- 각 순환 호출에서는 전체 리스트의 대부분의 레코드를 비교해야 하므로 평균 n번 정도의 비교가 이루어짐
- 최악의 시간복잡도 = 순환 호출의 깊이 * 각 순환 호출 단계의 비교 연산 = n^2
- 이동 횟수는 비교 횟수보다 적으므로 무시할 수 있다.
- 평균의 경우 O(nlog₂n)
공간복잡도
- 주어진 배열 안에서 교환을 통해 정렬이 수행되므로 O(n)
장점
- 불필요한 데이터의 이동을 줄이고 먼 거리의 데이터를 교환할 뿐만 아니라, 한 번 결정된 피벗들이 추후 연산에서 제외되는 특성 때문에, 시간 복잡도가 O(nlog₂n)를 가지는 다른 정렬 알고리즘과 비교했을 때도 가장 빠르다.
- 정렬하고자 하는 배열 안에서 교환하는 방식이므로 다른 메모리 공간을 필요로 하지 않는다.
단점
- 불안정한 정렬이다.
- 정렬된 배열에 대해서는 Quick Sort의 불균형 분할에 의해 오히려 수행시간이 더 많이 걸린다.
참고 출처 1 : https://babbab2.tistory.com/101
참고 출처 2 : https://gyoogle.dev/blog/algorithm/Quick%20Sort.html
반응형
'🔡 Algorithm' 카테고리의 다른 글
| [Algorithm] Insertion Sort (삽입정렬) by Swift (0) | 2022.01.15 |
|---|---|
| [Algorithm] Selection Sort (선택정렬) by Swift (0) | 2022.01.11 |
| [Algorithm] Bubble Sort (거품정렬) by Swift (0) | 2022.01.10 |